Three Drawings and one Story
Frieder Nake
When you grab any two images and put them side by side, and assume – as a minimal assumption – that the two were done by one and the same person, and when you now compare them, looking at the left one, looking at the right one, and back again, and left and right, and you do this for some while, then chances may well be that you discover some similarities between the two images, however vague and weak they may be. I would definitely like to do this, celebrate such an exercise on, say, two or three randomly chosen pairs of images from three different persons, artists or not, and observe in this experiment (whose subject matter – or rather object I would clearly be myself!), what would happen to me, what would I discover, deliberately or accidentally, laughingly or intentionally. It could be fun, but it could also be boring, and my friends would shake their heads and ask why, the hell, I was doing this, did I not have anything better to do, or rather nothing, perhaps, why not just sit down, drink a good grappa and enjoy yourself. And, frankly, I would not know either, why I would be doing this, but I would nevertheless say, I like doing it, because I thought of it when Wolf Lieser, the handsome tall gallerist, asked me whether I would write the story of those two images that you may see here. And they are drawings.
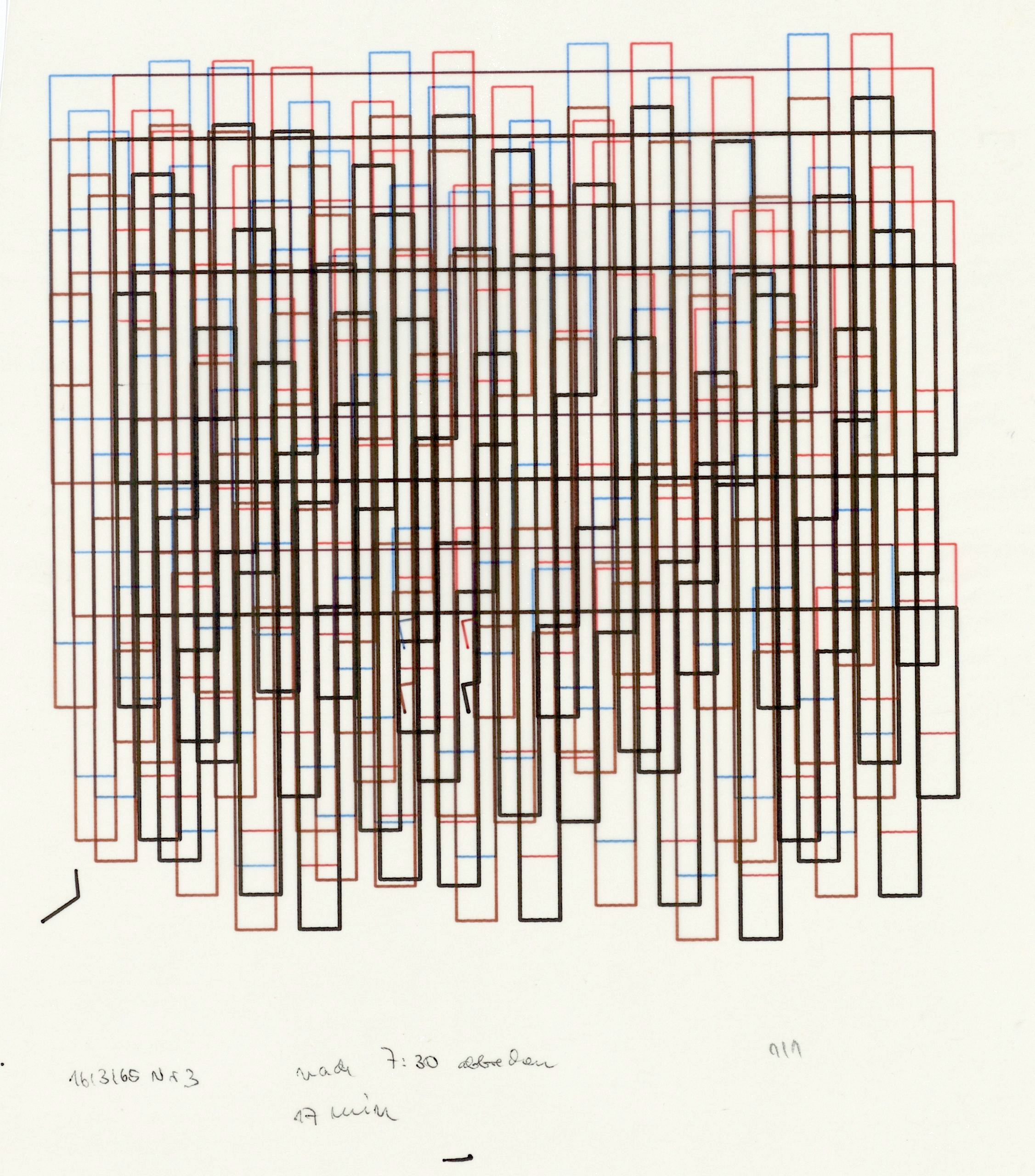
Obviously, both drawings are made up exclusively of horizontal and vertical lines in four different colors, which is a conjecture, not quite certain. Some of the lines are short, some longer, they form to dense areas, and not quite so dense areas. These are some characteristics constituting kinds of similarities I was talking about, and there may be, upon more detailed inspection, some more similarities of this kind.
But there are also differences, some standing out. The left drawing shows a number of horizontal lines running across the entire width of the image which may be an event in the right image, too, but if it is, then it is not as conspicuous. There are definitely rather dark areas in the right image, and some quite thinly populated areas also (in the upper region). In comparison, the left-hand drawing displays, in some sense, a more homogeneous density of lines. Do you share this with me? Is the left drawing more “structured”, perhaps, and the right one more “chaotic”? Could I claim and uphold such a statement? I think, I could do so. If you agree, I love you. If you don’t, it doesn’t really matter, and, in a way, it’s all the same.
Pretty boring, such descriptions, do you agree? Yes. But I am sorry, what else could I come up with? An analysis of this style is taking into consideration only the surface of those two images. The “surface” is what we may claim to see immediately, in the same way as some scanning mechanism would “see” these images. That’s why this is so boring. Let us try a second time.
You may discover some regularities in the use of colors, more so and easier, in the left than in the right image. Look at the top of the left one! See the light blue and the light red peaks there? Somehow, they are always neighbors of each other. Once you have observed this, you start looking for more of it, and you discover more, even though I believe, this is not easy. Some speculation may make you try to discover, in the right image, similar neighborhood relations or other kinds of relations in all the chaos of the red and blue and other lines. What are the black lines doing? And now you discover, there is even a fourth kind of colored line, harder to detect in the first place, but they are there. There seems to be good reason for some degree of conjecture or speculation. Isn’t that what you expect of an image?
Some say, there must be “meaning” in the image. The image must tell us something. The form aspects? Okay, take them for granted. But should they not come-with? Should they not carry a meaning. Yes. No. Concrete art is what it is and nothing else. And it is up to you what you see. Including the option that you see nothing, and, definitely, you may see something else.
Jump! You read, in the captions of the two images, the titles of those two very simple drawings. E.g., “16/3/65 Nr. 3”. That’s an easy to decode schema. It says: This was drawing no. 3 on the 16th of March in 1965. Similarly, the other one, to the right: No. 11 on the 20th of February 1965. Alright. You, my reader, may know, that this is the time when Georg Nees, for the first time in the world, exhibited computer-generated graphics (it so happened from February 5 to 19, 1965, at Studien-Galerie der TH Stuttgart). There was a second such exhibition – showing images by A. Michael Noll and Bela Julesz – whose opening was still some weeks into the future (it took place from April 6 to 24, 1965, at the Howard Wise Gallery in New York City[1]). According to their dates, our two images of interest in this essay were generated between those two historic events. But the two images did already exist then when computer art happened. They are of algorithmic origin, and should be considered, with due modesty, as carrying the attribute of historic relevance. And, by the way, they are in color which distinguishes them from what you could see at the two other shows mentioned. Nothing to be much excited about …
You may have heard of the following little anecdote which is at the origin of my contribution to the emergence of computer art, as it was called and still is, even though a term like algorithmic art more distinctly and correctly describes what is characteristic for this kind of aesthetic objects. “Generative art” is another favorite term. It was actually used by Max Bense in the context of Georg Nees’ show.
Here is the anecdote. One morning in the summer or fall of 1963, the director of the Computing Center of the University of Stuttgart, Prof. Walter Knödel, told me that it had been decided that the Center would acquire a drawing machine. Pause. I was a student of mathematics not far from graduating. My job for the Center was to develop and test software for numerical mathematics, and to look after the program library which, by the time, was a rather different affair if compared to now. Everything was (still) done in machine language (a condition that soon was over).
Why was Knödel telling me about this acquisition of a “drawing machine”, I wondered. And what would that be, a “drawing machine”? I did not ask him, and he continued telling me that the drawing machine they would get was a brand-new construction by Konrad Zuse, the inventor of the programmed computer. It was creating very precise lines, and it should become a great help for many of the engineering researchers who would become able to depict results of their numerical calculations instead of running through columns of numbers in search of deviations, errors, or other unexpected behaviors of mathematically defined systems. This was mildly interesting to me, but as a young mathematician, I did not like the engineers all too much because it seemed they often did not really know what they were doing with our large machines.
Prof. Knödel, in our short exchange, moved on to the highlight of his announcement and to the reason why he had come to meet me. He revealed that the Center would not get any software for the drawing machine, because the Zuse Company manufactured their own computers, and their software for drawings was for those computers, not others. Prof. Knödel ended by asking me, in his friendly Viennese accent: “Would you develop that software?” With no hesitation, I heard me saying, “yes.”
He left. I sat down. What am I going to do now, I asked myself. I had, of course, not a clue of an idea what it would mean to develop – for all possible customers of this university – a software package for all their drawing jobs, yet unknown. I would have to find out what that software could possibly be. I also needed to learn how to control that alien monster never seen, the “drawing machine”. What were its specifications and characteristics, and how would I establish a bridge between the computer and this new machine that was about to transform the computing into a drawing machine, numbers into lines, the clear symbolic into the vague iconic.
Of course, I had, by the time, no clue of Ivan E. Sutherland’s doctoral thesis that he had submitted to MIT earlier the same year, under the title, Sketchpad. A man-machine graphical communication system. Only two years later, when my good fortune had told me I was now a computer graphics novice, did I become aware of this wonderful world were computers were calculating in order to draw, and of Sutherland’s tremendously important and ingenious work [2]. In those young years of the decade of the 1960s, the roots were planted for what we now call digital media: not less than a cultural revolution! Three years later, China began the Great Proletarian Cultural Revolution. The digital won.
Nothing better has ever happened to me than this short meeting of five minutes in 1963, when Prof. Knödel entrusted me with a task I had no idea of how to do it. It was the trust of an exceptional teacher that got me into this. He knew as little as I did of how the computer would become able to draw. But he believed his student would do it. This was teaching by not knowing better. During my academic career, I have tried to follow Prof. Knödel a bit at least – trusting students rather than mistrusting them. Isn’t this what teaching should be about?
Important, in a different way, for the career that was now opening up for me, was inspiration by the work and teaching of Max Bense, the philosopher in Stuttgart. During the 1950s, he was developing his own aesthetics under the name of Information Aesthetics. Its foundation was the hypothesis, first, that the aesthetic object was a sign that carried a particular kind of information: “aesthetic information”. And second, that important properties of aesthetic objects could (and must) be measured by methods similar to those of physics. Shannon’s and Weaver’s theory of communication (and information) became one pillar of Bense’s aesthetics, and Gary D. Birkhoff’s macro-aesthetic measure of “order in complexity” became the other one. Between 1954 and 1960, Bense published four volumes of his Aesthetica. And in 1965, they were put together in one volume to which Bense added a short essay on generative aesthetics [3].
As a student of mathematics, I went to all of Bense’s lectures and thus was well prepared (without knowing it) for the new job: Develop the software for the new drawing machine, the Zuse Z64 “Graphomat”. Before I had even seen this machine, I had the software ready to be tested and run on the actual machine as soon as it would arrive. What it would first be tested on would be polygons of a heavily random kind.
The flatbed drawing machine had a resolution of one sixteenth of a millimeter in each of four primary directions (left / right, up / down). The sixteenth was realized by the sixteen speed levels which two step-motors could be driven by. Considering the first quadrant of the coordinate system alone (where coordinates x and y are both non-negative), we have 225 different directions that can be drawn exactly. All other directions must be approximated by alternating the given ones. No detail of the algorithm [4] behind this is interesting for our discussion with one exception. When it came to test the software, I decided not to systematically try those different directions. I rather did it randomly. I trusted that, by choosing directions randomly, sooner or later all directions would appear. I would not know which ones were appearing when. But aesthetically, it would be much more exciting this way. And it was.
Let us take another look of one of our two images (see below). It now contains some hand-written remarks that were cut off in the reproduction above. (You can see the remarks enlarged below the image.) In addition to the title,”16/3/65 Nr 3″, we see the typical “1/1” from the world of graphics production in fine art. It says that, of a total edition of only one piece, this is the one and only. More interesting than this, however, is the note “nach 7:30 abbrechen / 17 min” [5] . What does this say?
Our reproduction does not show that the paper of the image is transparent paper. This was the kind of paper I was using for test-runs. The note on that drawing (a note to myself) tells us that the drawing machine took 17 minutes in total to draw what the computer had calculated before. This statement makes sense only if we are aware of the fact that the two machines – digital computer and drawing machine – were working independent of each other. The computer was running the program whose result was a punched paper tape. This tape was taken to the room of the drawing machine. There, the tape was inserted into the tape-reader of the drawing machine such that this machine would now work by following exactly the commands on the tape.
I was taking the time needed by the drawing machine to complete the entire drawing; in this case, it took 17 minutes. I also put a note on the paper suggesting that, if I should run the same tape again through the drawing machine, I should stop it after seven and a half minutes already. Probably, I had observed that, at this time, the drawing had reached a state that I thought, was good or interesting or pleasing enough. This was, of course, a completely subjective statement, and also absolutely against any idea of autonomy on behalf of the machines. Obviously, I wanted to run experiments and keep control of final decisions. Even if this particular decision is a very simple one, and the computing and drafting machines were doing the bulk of all the work, I decided what was to be offered to the public.
Clearly: I was the artist! A laughable artist, to be sure. An artist of a new kind, if you like, who was making use of incredibly complex and expensive equipment he himself would never be able to afford. But an artist insofar as he – like all other artists – decided when an image was finished or whether it was finished at all and not rather to be thrown away. I developed the general software, wrote the specific program, set the parameters for running the program. This concerns the generative process. I also kept for me the selective process: I influenced the process of materialization by choosing the paper, the pens, and the inks; and I finally selected the pieces that were to be destroyed or to leave the studio to be presented to the public.
Looking back from now, and not in anger, this innocent moment in Stuttgart, in March of 1965, with the, perhaps, silly note on the transparent paper, make up a document of historic importance. They document in the most minimal way the transgression from modern art to postmodern art, from hand and tool to mind and machine. We were entering the postmodern age, I don’t hesitate to claim, the age of the semiotic machine, of media controlled and run by algorithms, and collecting their own data to which they mediate.
You may have observed, in the lower left area of the image, right underneath the horizontal/vertical drawing matter, a funny small black hook that obviously does not belong there if there is any clear constructive intent in the image. And even more, but better hidden, you can detect smaller hooks, if you like, just below the lowest of the long horizontals running across, a bit left of the center. You see two of them, a black and a red one. Once you have become aware of those two, you see a third one occupying the lower left of this pattern. By now, you will guess that there must be a light blue one, and it is there, even though it is a bit hard to detect.
Why these? Don’t they violate the aesthetics of the image? Well, yes, they do according to one view well justified. And no, they don’t, because – is the artist not allowed to do whatever he or she is motivated to do? The answer to such thinking is, of course, that, from the algorithmic and pure view of an algorithmic construction, these are errors, whatever the particular reason of their existence may be. Given the simple construction of this trivial case of a drawing, the hooks come from somewhere but don’t belong into this image. They are no rebellion of the drawing against its own father, the algorithmic description, nor against its god, the human programmer.
However, we easily imagine that, given a less regular schema of the image, and a more chaotic appearance, then such events on the surface of a drawing may occur without raising issues like the question, “does some actual visual appearance belong to the visual surface, or is it nothing but a programming error or mishap during the visual procedure?” Would such an event then be of a different kind that those visual events that were caused by the algorithm? Would it allow to ascribe to the algorithm anything like its own decision-making?
Allow me to take the opportunity and draw your attention to yet one more algorithmic image from the same year of 1965, a few months later. Straight lines, massing up to the left, using the entire vertical extension of the format. Some vertical lines close to the middle, trying to do similar, but too weak to attain quite the same. And two forms spreading out much more into the open fields to the right half of the terrain, two forms clearly different in appearance, whatever they may be longing for. If you are friendly, you detect a plethora of more little events telling you their stories, if you still listen without being bored.
Not as strict as the vertical/horizontal design, color has been left out, more complexity can be observed. And yet, some features work against pure chaos. There are long and short lines, some very short only, and we feel some restrictions concerning the permitted directions. You already guess an answer, but I want to delay the final explicit formulation of it, in favor of a remark that may, I hope, surprise you a bit. This then is the (mild) surprise:
The three graphic images presented in this note come from one and the same program.
If this is so, we see here – in the case of a definitely trivial program – what the algorithmic approach to aesthetic experiments is capable of. It is capable of pulling together into one kind of operation rather different visual appearances and, thus, of experience. The algorithmic way of doing and thinking allows us to see (experience) commonalities in actions and operations that appear to be different only when the same type of operation is carried out on different data or objects.
What is the same, and what is different in our examples? All three are polygons. They differ only in the repertoire of permitted directions and lengths of lines. In order to use one and the same program to generate all three images, we only need a way to describe the sets of permitted directions and lengths of the consecutive edges of the polygons.
The permitted directions in the first two experiments are, starting from the horizontal and going to the right taken as 0 degree: 0, 90 (down), 180 (left), and 270 (up). In the third example, the directions are: 0, 60, 90, 120, 180, 240, 270, 300 degrees.
In the first two results, the choice of the direction took turns: horizontal, vertical, horizontal etc. In Fig. 1, horizontal direction, the distance to go was determined by an extraordinary random-number generator that gave almost the same short length to progress to the right, but then be reflected back to the far left when the right-hand boundary of the image was reached. In vertical direction, the line would randomly go down or up for a short or long distance.
The second horizontal/vertical drawing (Fig. 2), in its horizontal direction, did not have the restriction in distance but chose it at random.
More variety was given to the third polygon in choice of direction (Fig. 4). Now, there were eight permitted directions, and also more open choice of distances (with the condition only, that the drawing had to stay within the image plane). I must, however, add a remark concerning the vertical direction (90 or 270 degrees). The vertical had the option of varying a bit to the left or right, by a few degrees only (it may have been ± 3 degrees).
Not much more is to be said about these drawings. We may precisely make explicit all the secrets of an algorithmic aesthetic object. Otherwise, it would not be algorithmic. We can, nevertheless, use strict structural conditions to generate interesting aesthetics. What we need for this, is randomness or chaos.
The task of art today is to bring chaos into order.
(Theodor W. Adorno, 1970)
Frieder Nake is an artist and mathematician, one of the earliest pioneers of algorithmic art.
This text was written for DAM Gallery, Berlin, March 2020.


